Exponents

The exponent of a number says how many times to employ the number in a multiplication.

8 to the Power 2

In viii2 the "two" says to use 8 twice in a multiplication,
so 82 = 8 × 8 = 64

In words: 82 could be called "8 to the power 2" or "8 to the 2d ability", or merely "viii squared"

Exponents are likewise chosen Powers or Indices.

Some more examples:

Example: 53 = 5 × v × 5 = 125

  • In words: 53 could be chosen "5 to the third ability", "five to the ability 3" or simply "5 cubed"

Example: two4 = 2 × 2 × ii × ii = 16

  • In words: ii4 could exist called "ii to the 4th power" or "2 to the ability 4" or simply "2 to the 4th"

Exponents make it easier to write and employ many multiplications

Example: 9vi is easier to write and read than 9 × ix × 9 × 9 × ix × 9

You can multiply whatsoever number by itself as many times as yous want using exponents.

Try here:

algebra/images/exponent-calc.js

Then in general:

anorth tells you to multiply a by itself,
and then there are n of those a's:		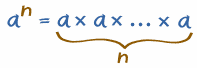 exponent definition

Another Way of Writing It

Sometimes people use the ^ symbol (higher up the half-dozen on your keyboard), every bit information technology is easy to type.

Instance: 2^4 is the same as 24

  • 2^4 = 2 × two × 2 × 2 = 16

Negative Exponents

Negative? What could be the opposite of multiplying? Dividing!

And then we divide by the number each time, which is the same as multiplying by i number

Instance: 8-1 = i 8 = 0.125

We tin keep on like this:

Example: 5-3 = one 5 × 1 five × 1 5 = 0.008

But it is oft easier to do it this mode:

v-3 could also exist calculated like:

1 v × v × five = one 53 = 1 125 = 0.008

Negative? Flip the Positive!

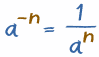negative-exponent

That last instance showed an easier way to handle negative exponents:

  • Calculate the positive exponent (an )
  • And then have the Reciprocal (i.e. 1/an )

More Examples:

Negative Exponent Reciprocal of
Positive Exponent		 Reply
iv-2 = 1 / 42 = i/16 = 0.0625
10-3 = one / ten3 = ane/1,000 = 0.001
(-2)-3 = 1 / (-2)3 = 1/(-8) = -0.125

What if the Exponent is 1, or 0?

1 If the exponent is one, then you just have the number itself (instance ixone = nine)
0 If the exponent is 0, and so you get i (instance nine0 = 1)
But what nigh 00 ? It could be either 1 or 0, and so people say information technology is "indeterminate".

It All Makes Sense

If you look at that table, y'all will see that positive, cypher or negative exponents are really part of the aforementioned (fairly elementary) pattern:

Case: Powers of 5
.. etc.. exponent 5 times larger or smaller
v2 5 × 5 25
51 5 five
50 ane i
five-i 1 5 0.two
5-ii i 5 × 1 5 0.04
.. etc..

Exist Conscientious About Grouping

To avert confusion, use parentheses () in cases like this:

With () : (−2)2 = (−2) × (−2) = 4
Without () : −ii2 = −(2ii) = −(2 × 2) = −4

With () : (ab)2 = ab × ab
Without () : ab2 = a × (b)2 = a × b × b

305, 1679, 306, 1680, 1077, 1681, 1078, 1079, 3863, 3864